다익스트라 알고리즘 ( Dijkstra Algorithm )

Reference : https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/

 

다익스트라 알고리즘은 그래프를 이용한 그리디 알고리즘 중 하나이다. 

다익스트라 알고리즘은, 주어진 그래프에서 한 점에서 모든 정점까지의 최단경로를 찾는다. 

 

- 시간복잡도 ( Time Complexity ) : O( V^2 ) ( V : 정점 개수 )

- 공간복잡도 ( Space Complexity ) : O( V ) ( V : 정점 개수 )

 

다익스트라 알고리즘의 경우, Prime`s MST ( Minest Spanning Tree )  알고리즘과 유사하다. 

루트를 기준으로, 두 집합을 유지한다. 

한 집합은 최단경로트리에 포함된 정점을 포함하며,

다른 집합은 최단경로트리에 아직 포함되지 않은 정점을 포함한다. 

알고리즘의 모든 단계에서 다른집합 ( 아직 포함되지 않은 집합 ) 에 있고 루트로부터 최소 거리를 가진 정점을 찾는다.

 

아래 예시를 살펴보자.

 

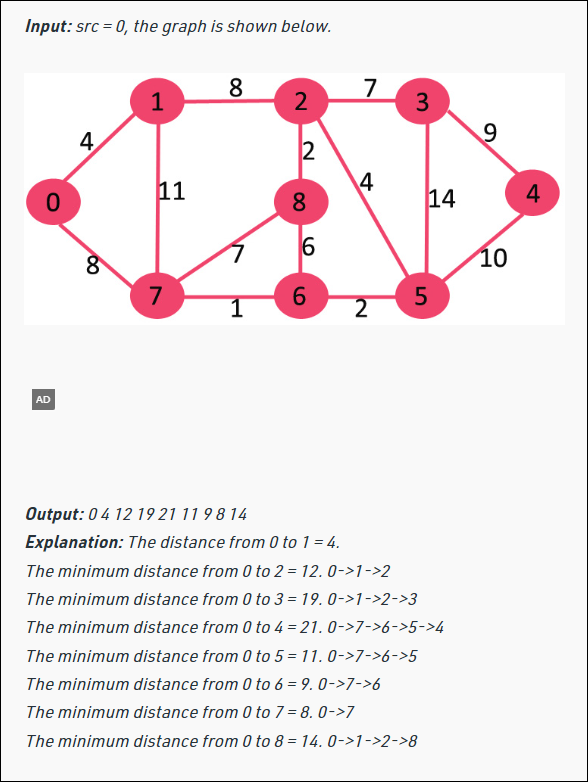
위 그래프를 예시로 들었을때, 출발지를 0번 정점이라고 잡았을때, 각 정점까지의 이동했을때 들어가는 최소비용(최단거리) 를 나타낸 그림이다. 

 

어떤식으로 저렇게 각 정점까지의 최단거리를 구하는지 한 단계씩 알아보자. 

 

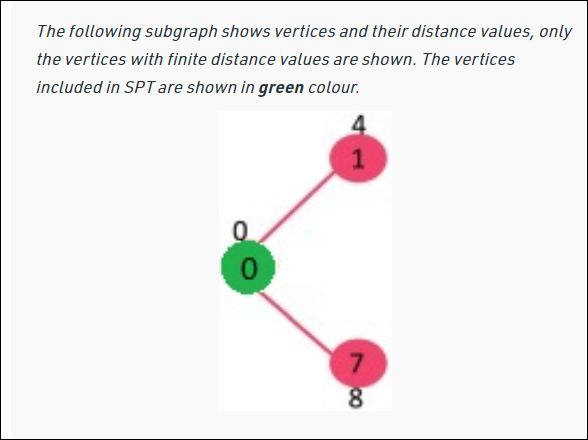
1. sptSet ( shortest path tree : 최단경로트리 ) 를 세팅시켜준다. => 각 정점까지의 최단거리가 계산되고 계속 정점을 추적해서 갱신하는 트리

2. 입력 그래프의 모든 정점에 거리 값을 할당한다. 처음에는 모든 거리값을 INFINITE 로 초기화한다. 처음 시작점으로 선택된 정점의 경우, 거리를 0으로 세팅한다.

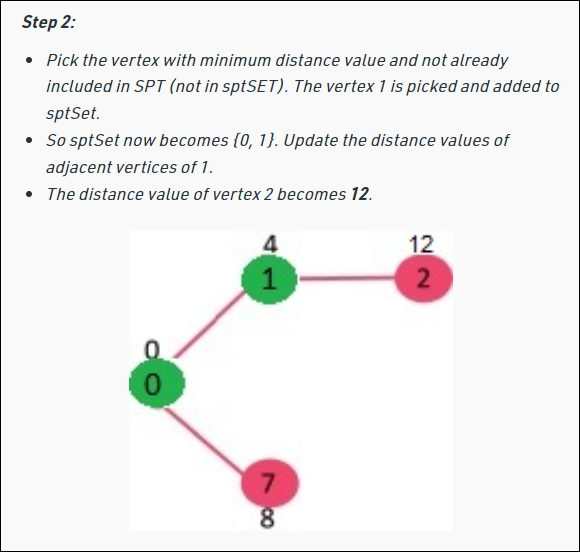
3. sptSet 은 최소거리 값을 가진 정점 u를 세팅한다. ( 따라서 모든 정점을 포함하지 않을 수 있음 ) 

4. 다음으로, 정점 u 의 모든 인접 정점의 거리값을 업데이트 한다. 

거리값을 업데이트 하려면, 인접한 모든 정점도 살펴본다. 

5. 인접한 정점을 v라고 할 때, u 정점에서 모든 인접한 v 까지의 거리의 합이 가장 작은경우가 있다면, 현재 v값을 갱신한다. 

 

이런 방식을 위 그림에 적용해보자. 

 

 

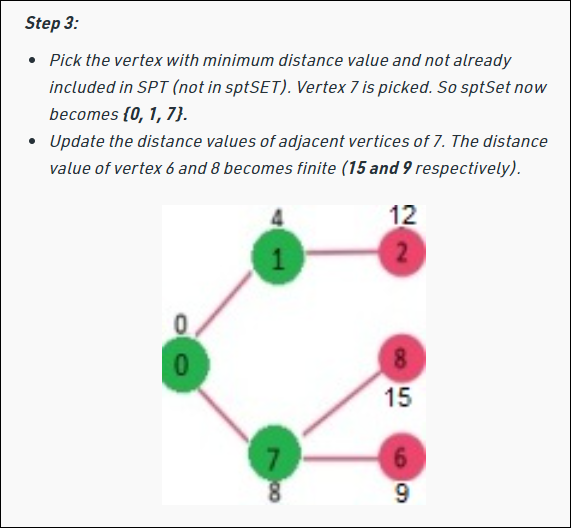
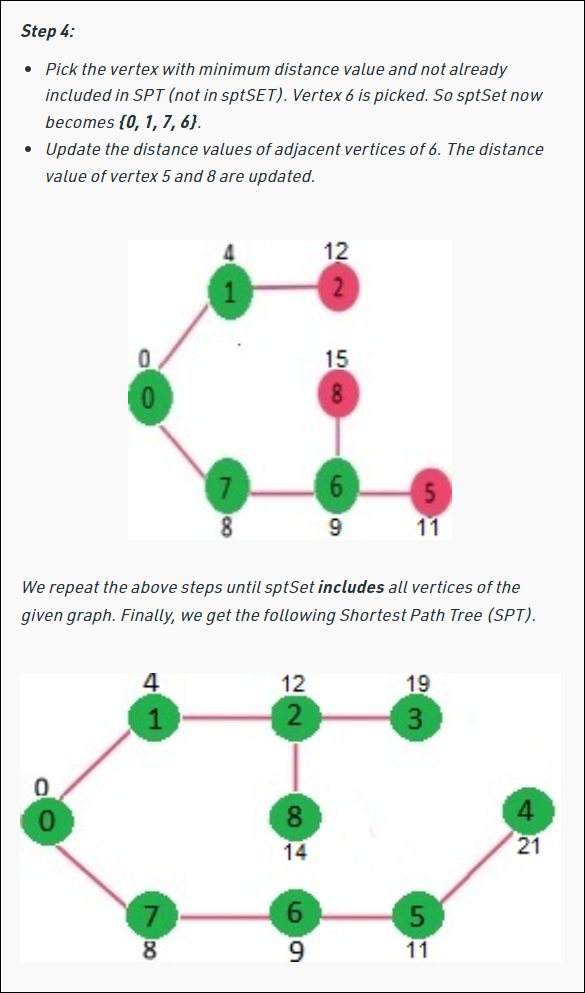
이제 코드로 구현해보자. 

 

#include <iostream>

#include <limits.h>

using namespace std;

#define MAX_V 9

// Find the vertex with minimum distance value,

// from the set of vertices not yet included

// in shortest path tree

int minDistance(int dist[], bool sptSet[])

{

    // Initialize min value

    int min = INT_MAX;

    int min_index;

    for (int v = 0; v < MAX_V; ++v)

    {

        if (sptSet[v] == false && dist[v] <= min)

        {

            min = dist[v];

            min_index = v;

        }

    }

    return min_index;

}

void printSolution(int dist[])

{

    cout << "Vertex Distance from Source\n";

    for (int i = 0; i < MAX_V; ++i)

    {

        cout << i << " " << dist[i] << '\n';

    }

}

void dijkstra(int graph[MAX_V][MAX_V], int src)

{

    // output array. dist[i] will hold the

    // shortest distance from src to i

    int dist[MAX_V];

    // sptSet[i] will be true if vertex i is included in

    // shortest path tree or shortest distance from src to i is finalized

    bool sptSet[MAX_V];

    // Initialize all distances as INFINITE and sptSet[] as false

    for (int i = 0; i < MAX_V; ++i)

    {

        dist[i] = INT_MAX;

        sptSet[i] = false;

    }

    // Distance of source vertex from itself is always 0

    dist[src] = 0;

    for (int count = 0; count < MAX_V - 1; ++count)

    {

        // Pick the minumum distance vertex from the set of

        // vertices not yet processed.

        // u is always equal to

        // src in the first iteration

        int u = minDistance(dist, sptSet);

        // Mark the picked vertex as processed

        sptSet[u] = true;

        // Update dist[v] only if is not in sptSet,

        // there is an edge from u to v, and total

        // weight of path from src to v through u is

        // smaller than current value of dist[v]

        for (int v = 0; v < MAX_V; ++v)

        {

            if (!sptSet[v] && graph[u][v]

                && dist[u] != INT_MAX

                && dist[u] + graph[u][v] < dist[v])

            {

                dist[v] = dist[u] + graph[u][v];

            }

        }

    }

    printSolution(dist);

}

int main()

{

    // Example graph

    int graph[MAX_V][MAX_V] =

    {

        { 0, 4, 0, 0, 0, 0, 0, 8, 0} ,

        { 4, 0, 8, 0, 0, 0, 0, 11, 0 },

        { 0, 8, 0, 7, 0, 4, 0, 0, 2 },

        { 0, 0, 7, 0, 9, 14, 0, 0, 0 },

        { 0, 0, 0, 9, 0, 10, 0, 0, 0 },

        { 0, 0, 4, 14, 10, 0, 2, 0, 0 },

        { 0, 0, 0, 0, 0, 2, 0, 1, 6 },

        { 8, 11, 0, 0, 0, 0, 1, 0, 7 },

        { 0, 0, 2, 0, 0, 0, 6, 7, 0 }

    };

    dijkstra(graph, 0);

    return 0;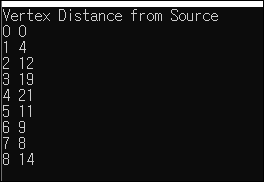

}

 

 

 

 

-----------------------------------

 

단, 다익스트라 알고리즘의 경우, 음수간선이 있는 그래프에서는 사용할 수 없기에 그래프가 어떤식으로 구축됬는지에 따라 쓸 수 있을수도 있고 없을수도 있다.